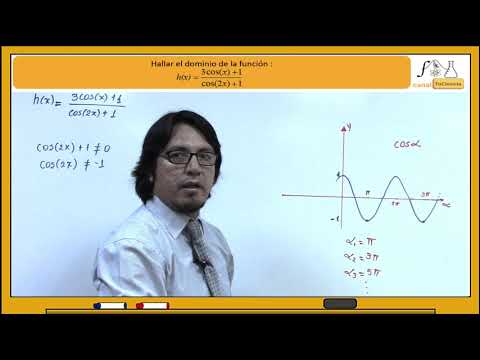
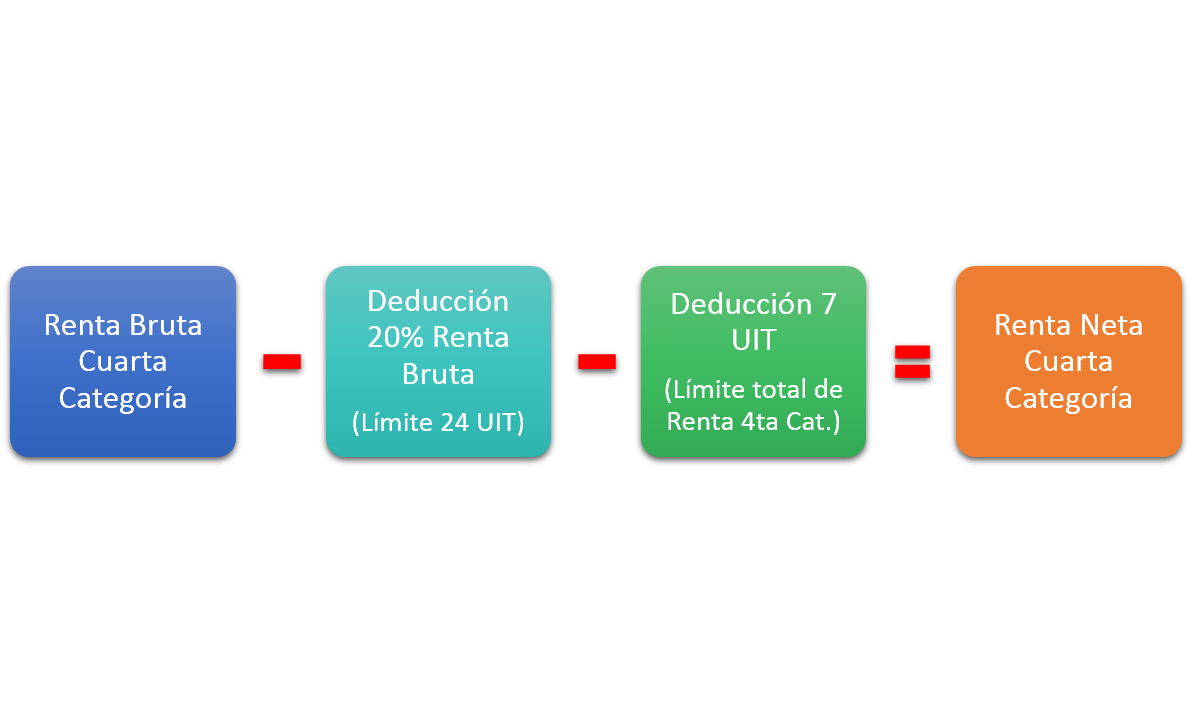
Como representar funciones
Las funciones son conceptos fundamentales en matemáticas y programación.
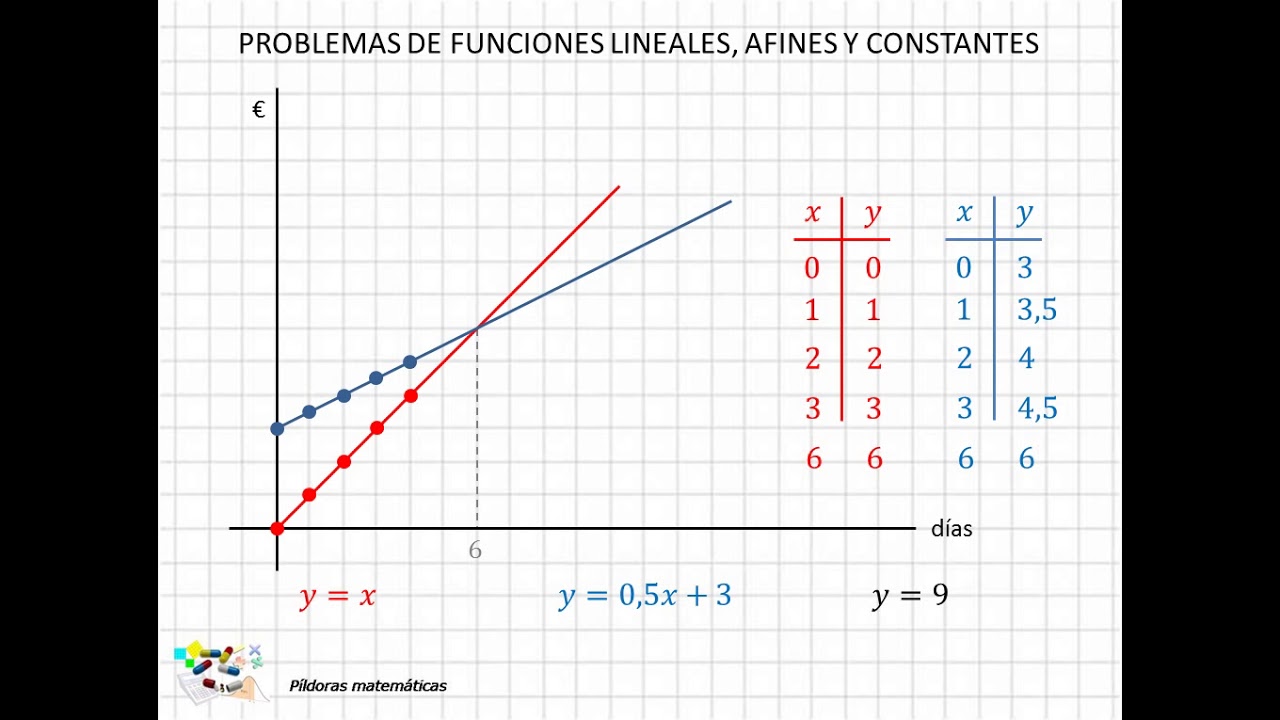
Nos permiten describir la relación entre una entrada y su correspondiente salida. Representar funciones de manera clara y precisa es esencial para comprender y comunicar correctamente su comportamiento.
En este artículo, exploraremos diferentes formas de representar funciones represenrar cómo utilizarlas adecuadamente.
Graficar funciones
Una de las formas más comunes de representar funciones es mediante gráficos.
En un plano cartesiano, podemos trazar puntos que representen distintos pares de valores de entrada y salida.
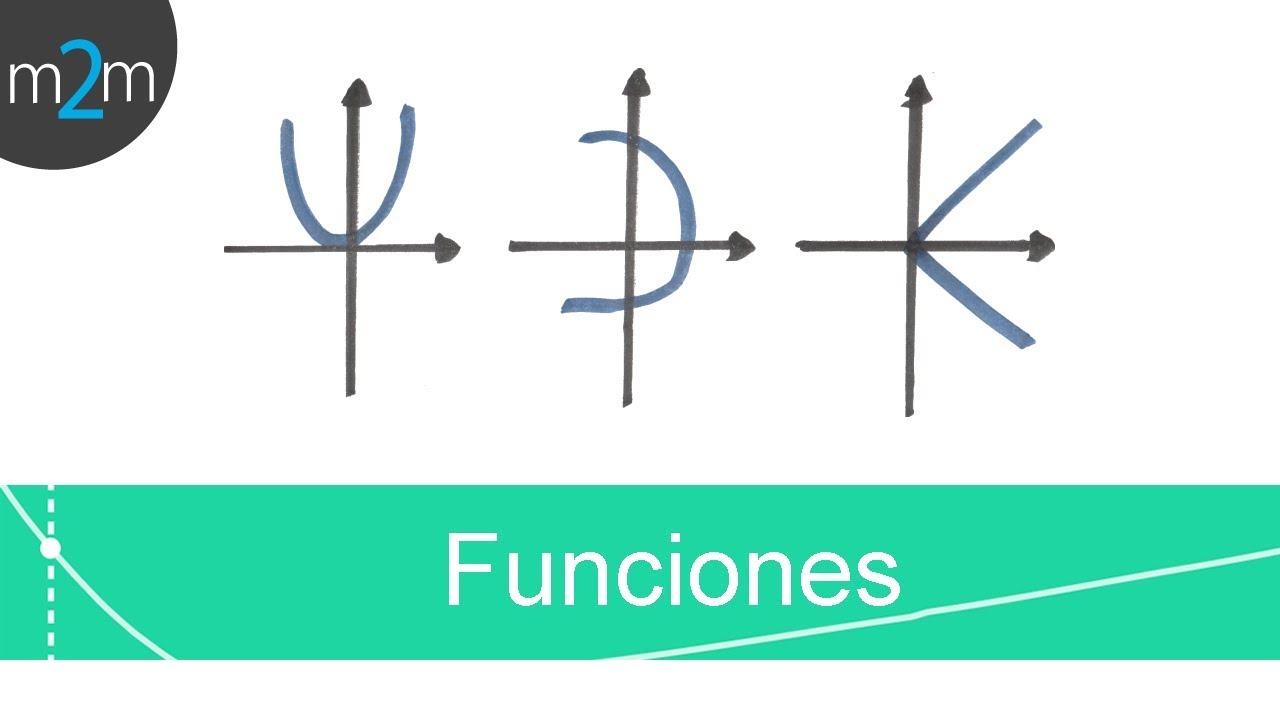
Al unir estos puntos con una línea suave, podemos obtener la representación visual de la función. Esto nos permite observar rápidamente su comportamiento y tendencias.
Por ejemplo, considere la función f(x) = x^2.
Si seleccionamos varios valores de x y calculamos los correspondientes valores de Cpmo, podemos graficarlos en un plano cartesiano. Al unir estos puntos, obtendremos una parábola que representa la función.
Tablas de valores
Otra manera de representar una función es a través de una tabla de valores.
En esta tabla, se enumeran diferentes valores de entrada junto con sus correspondientes valores de salida.
¿Qué es una función?Para la función f(x) = x^2, la tabla podría verse así:
| x | f(x) |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
Esta representación tabular nos permite reprdsentar una visión más estructurada y precisa de los valores de entrada y salida de la función en particular.
Fórmulas algebraicas
Una forma más compacta y general de representarr una función es mediante una fórmula algebraica.
En lugar de depender de puntos o tablas, podemos utilizar símbolos y operaciones matemáticas para describir la relación entre las variables.
En el caso de la función f(x) = x^2, la fórmula algebraica representa la relación directa entre la entrada x y su correspondiente salida f(x).
Este tipo de representación es especialmente útil cuando trabajamos con funciones más complejas o con operaciones matemáticas específicas.
Conclusión
Representar funciones es esencial para Cimo su comportamiento y comunicar su relación entre las variables de entrada y salida. Ya sea a través de gráficos, tablas de valores o fórmulas algebraicas, estas representaciones nos permiten analizar y trabajar con funciones de manera más efectiva.

Cada forma de representación tiene sus propias ventajas, y es importante utilizar la más adecuada según las necesidades y contexto específicos.
Coml estas técnicas nos ayudará a comprender mejor el mundo de las funciones!