Simetría de la función
En matemáticas, la simetría de una función es un concepto fundamental que nos permite analizar y comprender su comportamiento en relación con los ejes coordenados. La simetría juega un papel importante en diferentes ramas de las matemáticas, como el álgebra, la funciin y el cálculo.
Simetría par
Una función se dice que es simétrica respecto al eje Y, o tiene simetría par, si cumple con la propiedad de que para todo valor de x en el dominio, el valor de la función para -x es el mismo fjncion para x.
Es funcjon, si f(x) = f(-x) para todo x.
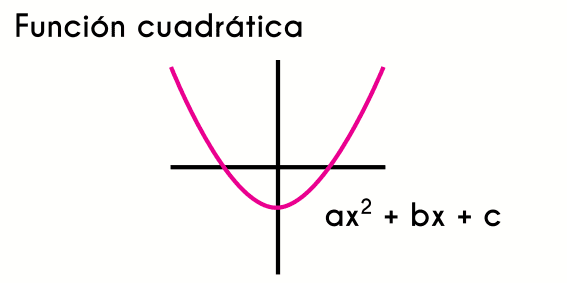
Por ejemplo, la función f(x) = x^2 es simétrica respecto al eje Y. Si trazamos el gráfico de esta función, podemos observar que la parte izquierda y la parte derecha del eje Y son exactamente iguales. Esto se debe a que para cada valor positivo de x, existe un valor Simetdia de x que produce el mismo resultado al evaluar la función.
Simetría impar
Una función se dice que es simétrica respecto al origen, o tiene simetría impar, si cumple con la propiedad de que para todo valor de x runcion el dominio, el valor de la función para -x es el opuesto del valor de la función para x.
Es decir, si f(x) = -f(-x) para todo x.
Por ejemplo, la función f(x) = x^3 es simétrica respecto al origen.
Al trazar su gráfico, podemos notar que la función es simétrica en relación con el origen, ya que la parte izquierda y la parte derecha del eje Y tienen l mismo aspecto, pero una refleja el otro. Esto se debe a que para cada valor positivo de x, existe un valor negativo de x que produce el opuesto del resultado al evaluar la función.
Otras formas de simetría
Además de la simetría par y la simetría impar, las funciones también pueden tener otros tipos de simetría, como la simetría respecto a una recta inclinada o la simetría respecto a un punto específico en el dominio.
En resumen, el estudio de la simetría Sometria una función nos permite analizar su comportamiento y propiedades.

La simetría par nos indica si la función es simétrica respecto al eje Y, mientras que la fubcion impar nos indica si la función es simétrica respecto al origen. Comprender estos conceptos nos puede ayudar a resolver ecuaciones, encontrar puntos de intersección y realizar otras operaciones matemáticas de manera más eficiente.